|
|
|
|
|
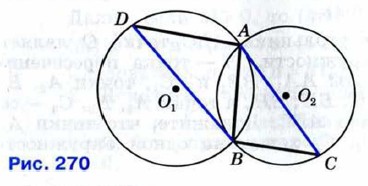
Глава VIII. Окружность Задачи повышенной трудности к главе VIII. Окружность877. Две окружности имеют единственную общую точку М. Через эту точку проведены две секущие, пересекающие одну окружность в точках А и A1, а другую — в точках В и В1. Докажите, что АА1 || ВВ1. 878. Прямая АС — касательная к окружности с центром O1, а прямая BD — касательная к окружности с центром О2 (рис. 270). Докажите, что: а) AD || ВС;
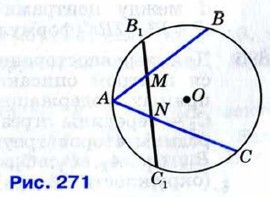
879. Точки В1 и С1 — середины дуг АВ и АС (рис. 271). Докажите, что AM = AN.
880. Окружность отсекает на двух прямых, которые пересекаются в точке, не лежащей на окружности, равные хорды. Докажите, что расстояния от точки пересечения этих прямых до концов той и другой хорды соответственно равны между собой. 881. Докажите, что для всех хорд АВ данной окружности величина 882. Через точку А пересечения двух окружностей с центрами в точках О1 и O2 проведена прямая, пересекающая одну окружность в точке В, а другую — в точке С. Докажите, что отрезок ВС будет наибольшим тогда, когда он параллелен прямой О1O2 883. Отрезок АВ является диаметром окружности с центром О. На каждом радиусе ОМ окружности отложен от центра О отрезок, равный расстоянию от конца М этого радиуса до прямой АВ. Найдите множество концов построенных таким образом отрезков. 884. Внутри угла АВС равностороннего треугольника АВС взята точка М так, что ∠BMC = 30°, ∠BMA = 17°. Найдите углы ВАМ и ВСМ. 885. Через каждую вершину треугольника АВС проведена прямая, перпендикулярная к биссектрисе угла треугольника при этой вершине. Проведённые прямые, пересекаясь, образуют новый треугольник. Докажите, что вершины этого треугольника лежат на прямых, содержащих биссектрисы треугольника АВС. 886. Пусть Н — точка пересечения прямых, содержащих высоты треугольника АВС, а А', В', С' — точки, симметричные точке Н относительно прямых ВС, СА, АВ. Докажите, что точки А', В', С' лежат на окружности, описанной около треугольника АВС. 887. Отрезок BD — биссектриса треугольника АВС. Докажите, что BD2 = АВ • ВС - AD • DC. 888. Из вершины В треугольника АВС проведены высота ВН и биссектриса угла В, которая пересекает в точке Е описанную около треугольника окружность с центром О. Докажите, что луч BE является биссектрисой угла ОВН. 889. Произвольная точка X окружности, описанной около равностороннего треугольника АВС, соединена отрезками с его вершинами. Докажите, что один из отрезков АХ, ВХ и СХ равен сумме двух других отрезков. 890. Докажите, что если диагонали вписанного четырёхугольника перпендикулярны, то сумма квадратов противоположных сторон четырёхугольника равна квадрату диаметра описанной окружности. 891. В четырёхугольнике ABCD, вписанном в окружность, биссектрисы углов А и В пересекаются в точке, лежащей на стороне CD. Докажите, что CD = ВС + AD. 892. Докажите, что площадь прямоугольной трапеции, описанной около окружности, равна произведению её оснований. 893. Докажите, что в любом четырёхугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея). 894. Докажите, что в любом треугольнике радиус R описанной окружности, радиус г вписанной окружности и расстояние d между центрами этих окружностей связаны равенством d2 = R2 - 2Rr (формула Эйлера). 895. Для неравностороннего треугольника АВС точка О является центром описанной окружности, Н — точка пересечения прямых, содержащих высоты АА1, ВВ1 и СС1, точки А2, В2, С2 — середины отрезков АН, ВН, СН, а точки А3, В3, С3 — середины сторон треугольника АВС. Докажите, что точки А11, B2, С3, А2, В2, С2, А3, В3, С3 лежат на одной окружности (окружность Эйлера). 896. Докажите, что основания перпендикуляров, проведённых из произвольной точки окружности, описанной около треугольника, к прямым, содержащим стороны этого треугольника, лежат на одной прямой (прямая Симпсона). 897. Постройте общую касательную к двум данным окружностям. 898. Даны окружность с центром О, точка М и отрезки P1Q1 и P2Q2. Постройте прямую р так, чтобы окружность отсекала на ней хорду, равную P1Q1, и расстояние от точки М до прямой р равнялось P2Q2. 899. Внутри окружности дана точка. Постройте хорду, проходящую через эту точку, так, чтобы она была наименьшей из всех хорд, проходящих через эту точку. 900. Постройте треугольник: а) по стороне, противолежащему углу и высоте, проведённой к данной стороне;
901. Постройте треугольник, если дана описанная окружность и на ней точки А, В и М, через которые проходят прямые, содержащие высоту, биссектрису и медиану треугольника, проведённые из одной вершины. 902. Даны три точки, не лежащие на одной прямой. Постройте треугольник, для которого эти точки являются основаниями высот. Сколько решений имеет задача?
|
|
|